1.2 DCM模型


DCM模型基于动态系统建模和贝叶斯统计框架，对神经网络中的有效连接模式及其调节机制进行研究。该模型将大脑抽象为一个复杂的“刺激输入—内部状态变化—输出响应”的动态系统，其中，外部环境的刺激作为输入，能够激发神经系统内部状态的动态演变，而这些内部状态的变化可以通过特定的输出信号得以体现。在这一理论架构下，DCM模型巧妙利用了给定的刺激输入与相应的输出反馈数据，通过调整模型的参数，逆向推断出隐藏于特定脑区背后的神经元活动变化及其相互间的有效连接模式。DCM模型中用于描述外界刺激下神经元状态变化的状态方程，其表达式如式(1)所示：

ż=F(z,u,θ)(1)

其中，ż表示神经元状态变量；F是描述外部输入刺激u或神经元活动z对其他脑区神经元状态变化产生生理影响的非线性函数；θ表示激活脑区生成模型中一系列待定的生物物理参数和连接参数；该方程反映了不同神经元集群之间的信息传递过程。


此外，基于观测方程，可以实现从目标脑区神经元集群活动状态到测量所得信号的进一步映射，其表达式如式(2)所示：

y=g(z,ϕ)(2)

其中，观测信号y通过观测函数g与隐含状态z及观测参数ϕ之间建立了明确的依赖关系。


在运用DCM模型解析神经元集群间有效连接模式的过程中，确保模型的神经生物学合理性是保障分析结果准确性的前提。这要求模型参数必须富含生物物理学信息，从而增加了参数估计的复杂性与挑战性。为了高效且可靠地实现对模型参数的估计，DCM模型采用了基于贝叶斯统计学的反演方法。


根据贝叶斯原理，对于特定的DCM模型m，其参数的后验概率密度p(θ|y,m)的计算，如式(3)所示：

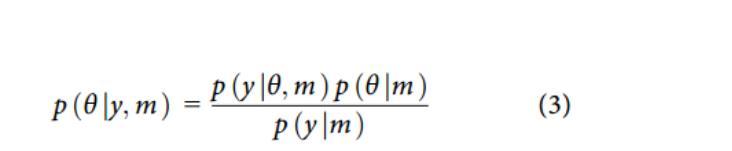
其中，p(y|θ,m)表示观测数据y在给定参数θ与模型m条件下的似然性；p(θ|m)作为参数的先验分布，融入了研究者对未知参数的先验知识；而p(y|m)，即模型证据值或边际似然函数，则综合评估了模型m对数据的整体解释能力，其在模型选择与评估中扮演着至关重要的角色。


基于模型证据值，可以对相同样本数据（如多脑区神经信号）所可能具有的不同连接模型的合理性进行比较。模型间的比较由贝叶斯因子体现，表达式如式(4)所示：

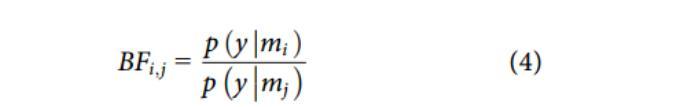
其中，mi和mj分别代表两种脑区间连接方式不同的DCM模型。贝叶斯因子BFi,j用于量化比较这两个模型与观测数据之间的拟合程度。具体而言，当BFi,j>1时，这指示了相较于模型mj，模型mi在解释观测数据方面展现出更高的证据支持，即模型mi与观测数据的匹配性更为优越。为解决由于多个贝叶斯因子相差过大而产生的难以表示的问题，可进一步对上式两边取对数，应用相对对数模型证据值进行表示，如式(5)所示：

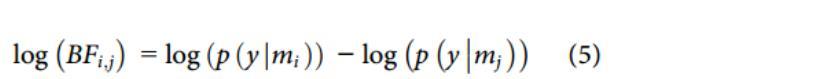
根据相关文献，本研究中假设同侧mPFC和vHPC之间存在双向连接。随后，应用贝叶斯反演和模型的相对对数证据值进行最优连接模型选择，并确定学习这一影响因素最可能对脑区间连接产生影响的情况，即最优调制模型；其中，相对对数模型证据值最大的模型，即为最优连接模型或最优调制模型。同时，基于模型后验概率评估所选最优连接模型和调制模型的置信度，当后验概率越接近1时，所选最优连接模型和最优调制模型的置信度越高。应用上述方法，本文对比分析了大鼠学习T迷宫记忆任务前后，以及正确和错误执行任务时，mPFC和vHPC之间连接强度的变化，探索了学习对相关脑区神经信息传递的影响。本文中的DCM模型分析使用英国伦敦大学学院开发的脑成像数据序列处理软件Statistical Parametric Mapping 12进行。


2结果


2.1 vHPC和mPFC间最优连接模型选择结果


如图2所示，为vHPC和mPFC之间的连接模型及贝叶斯模型选择结果。根据相关文献，同侧mPFC和vHPC之间可能存在5种不同情况的双向连接，分别为：模型1，两脑区之间存在双向前向连接；模型2，两脑区之间存在双向后向连接；模型3，vHPC到mPFC为前向连接，mPFC到vHPC为后向连接；模型4，与前一模型相反，mPFC到vHPC为前向连接，vHPC到mPFC为后向连接；模型5，两脑区之间同时存在双向前向连接和双向后向连接。本研究中，首先基于8只大鼠学习前和学习后执行T迷宫记忆任务时的LFPs数据，应用贝叶斯反演和模型的相对对数证据值进行上述模型的最优选择。贝叶斯模型选择结果显示，模型3具有最大的相对对数模型证据值（157），即vHPC和mPFC之间最优的连接模型为模型3（vHPC到mPFC为前向连接，mPFC到vHPC为后向连接）。进一步对该模型的置信度进行分析的结果显示，其后验概率为1，模型可信。因此，接下来，进一步基于模型3，对大鼠学习前后连接受影响的可能情况进行分析。

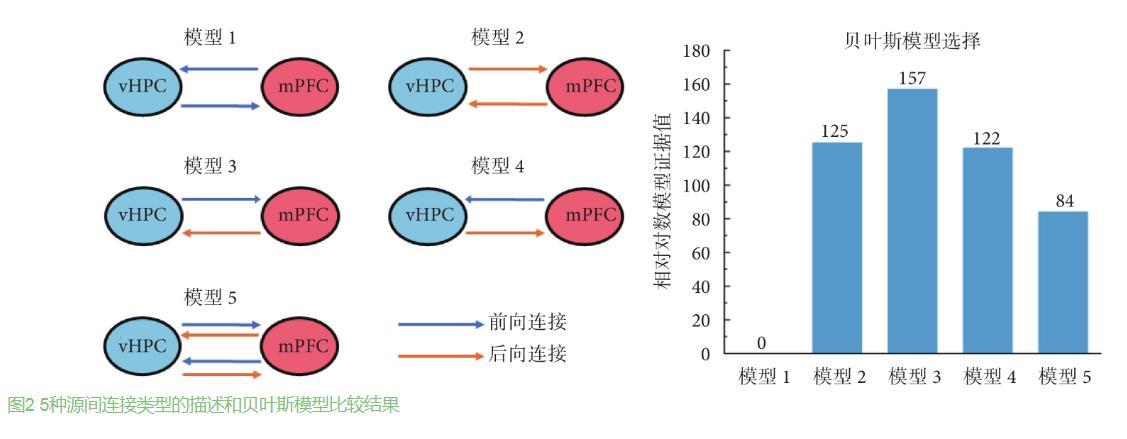
图2 5种源间连接类型的描述和贝叶斯模型比较结果


2.2最优调制模型选择结果


基于所选择的最优连接模型，学习这一因素对vHPC和mPFC之间连接的影响可能存在以下3种情况：一是仅vHPC到mPFC的前向连接受到影响；二是仅mPFC到vHPC的后向连接受到影响；三是两脑区之间的双向连接，即前向和后向连接均受到了影响。因此，所构建的连接调制模型如图3所示，其中，虚线表示受外界因素调制的脑区间连接，实线表示未受到影响的连接。同样，应用贝叶斯反演和模型的相对对数证据值对上述模型进行最优选择。图3右图连接调制模型中，横轴分别对应前向连接受影响、后向连接受影响、双向连接受影响的调制模型分析结果，纵轴为相对对数模型证据值。从图3中可以看出，双向连接均受到影响的模型具有最大的相对对数模型证据值（5.60），是最优的调制模型。进一步对其置信度进行分析的结果表明，该模型的后验概率为0.98，具有较高置信度（98%）。上述结果表明，对记忆任务的学习能够同时影响vHPC和mPFC之间的双向连接。

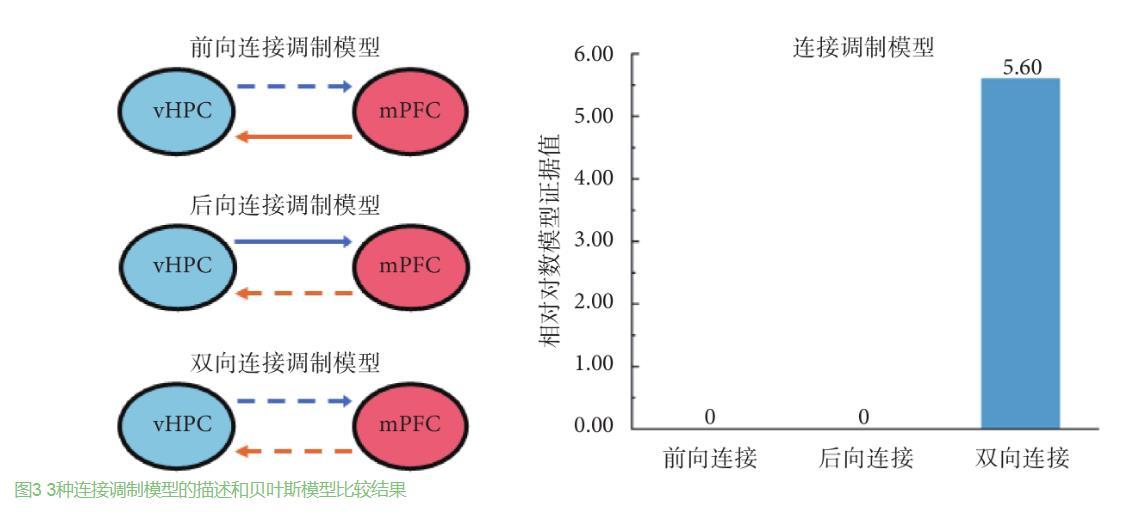
图3 3种连接调制模型的描述和贝叶斯模型比较结果